周志华《机器学习》习题解答：Ch5.10 - 卷积神经网络实验

发表于 | 分类于 | | 阅读次数:


本文基于python-theano实现了一个CNN模型，并用以解决MNIST手写字符识别实验（多分类）。

本系列相关答案和源代码托管在我的Github上：PnYuan/Machine-Learning_ZhouZhihua.

问题回顾

注：本题程实现基于python-theano（这里查看完整代码和数据集）。

基础知识回顾

CNN核心思想

卷积神经网络（Convolutional Neural Network, CNN）是“深度学习”的代表模型之一，是一种多隐层神经网络，正被广泛用于图像处理、语音识别等热点领域。

卷积神经网络的原理和特点，集中体现在以下三个核心思想当中：

  • 局部感受野（Local Receptive Fields）
  • 权值共享（weight sharing）
  • 时间或空间的亚采样

在整合了上述三大特点之后，卷积神经网络具备了很强的畸变容忍能力，能够从复杂的对象中隐式地进行特征提取与学习。

CNN结构和功能

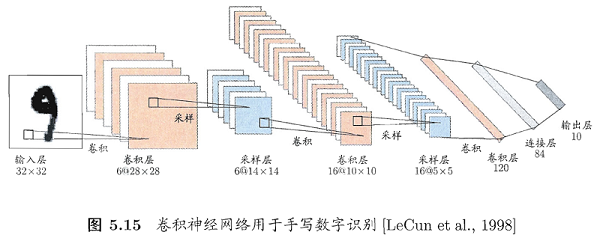
卷积神经网络同多层感知机（MLP）一样，通过设置多个隐层来实现对复杂模型的学习。如下图所示是一个手写字符识别的卷积神经网络结构示意图（书p114）：

从图中可以看到卷积层（convolutional layer）和采样层（pooling layer）的复合，其功能简述如下：

  • 卷积层包含多个特征映射（feature map），它们采用相应的卷积滤波器从输入中提取特征；
  • 采样层基于局部相关性原理对卷积层进行亚采样，从而在保留有用信息的同时减少数据量；

通过多层复合，隐层最终输出目标维特征向量，通过连接层和输出层输出结果。

CNN参数技巧

神经网络的参数设计十分重要，关于CNN模型的一些参数的考虑（如隐层特征图数目和大小、滤波器大小等），可参考Convolutional Neural Networks (LeNet)文章最后Tips and Tricks的内容。

手写字符识别实验

这里，我们采用python-theano深度学习库来实现基于MNIST数据的字符识别实验。关于theano的基础使用可参考：深度学习基础 - 基于Theano-MLP的字符识别实验（MNIST）。

数据获取及预处理

这里我们采用经过规约的数据集mnist.pkl.gz,给出该数据集的部分信息如下：

  • 维度属性：数据集包含3个子数据集，对应train_set、valid_set、test_set，样本规模分别为50000、10000、10000；每条样本包含：输入向量[1*784]，对应输入图片灰度矩阵[28*28]；输出值，对应图片类别标签(数字0-9)；
  • 完整度：样本完整；
  • 平衡度：未知；
  • 更多信息：手写字符所覆盖的灰度已被人工调整到了图片的中部。

下面是一些样例图片：

样例图片

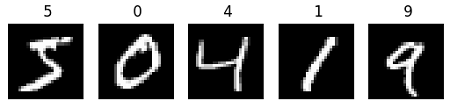
通过对数据集的分析，确定此处该数据集已无需额外的预处理即可使用，只是在使用时注意维度变换即可。

基于theano实现网络模型

基于theano来训练一个卷积神经网络需要完成的内容包括：

  1. 参数初始化，采用theano.shared来达到权值共享，基于数据信息设计相关参数（隐层规模、滤波器大小、学习率、迭代次数限、若采样MSGD算法还需设置mini-batch大小等）；
  2. 相关辅助函数，如采用theano.function实现tanh/sigmoid、似然损失函数等；
  3. 卷积操作（Convolution）和池化操作（pooling），采用theano.tensor.signal.conv2d实现二维（2D）卷积；采用theano.tensor.signal.pool.pool_2d实现最大池化（max-pooling），
  4. 训练过程优化机制，如加入不同时间尺度的验证、测试机制，早停机制；
  5. 实现迭代训练程序并得出模型（即最优参数）；

进一步地：

  • 将卷积层与池化层（采样层）整个为一个复合层，称为卷积-池化层（class LeNetConvPoolLayer）；
  • 将模型的训练、验证、测试整合在一个程序块中，方便早停判断；

这里还需进一步说明各层规模和滤波器大小的设置：

以当前样本为例，输入层大小[28*28]，若采用5*5的滤波器进行卷积，则第一个卷积层的特征图大小为[24*24]（ps. 28-5+1=24），若紧接着的亚采样模版大小为[2*2]，那么该池化层特征图大小为[12*12]（ps. 24/2=12）。同理，可计算出下一个卷积池化的特征图大小为[8*8]和[4*4]，再往后就只需要一个面向连接层的一维卷积层了，其节点数为当前的feature maps数。然后按照MLP模型给出连接层和输出层即可。

各层规模设置的样例程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
layer1 = LeNetConvPoolLayer(
    rng,
    input=layer0.output,
    image_shape=(batch_size, nkerns[0], 12, 12),
    filter_shape=(nkerns[1], nkerns[0], 5, 5),
    poolsize=(2, 2)
)    

layer2_input = layer1.output.flatten(2)

# construct a fully-connected sigmoidal layer
layer2 = HiddenLayer(
    rng,
    input=layer2_input,
    n_in=nkerns[1] * 4 * 4,
    n_out=500,
    activation=T.tanh
)

# classify the values of the fully-connected sigmoidal layer
layer3 = LogisticRegression(input=layer2.output, n_in=500, n_out=10)

给出该训练程序简化样例如下查看完整程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
def evaluate_lenet5(learning_rate=0.1,      # 学习率
                    n_epochs=200,           # 迭代批数
                    dataset='mnist.pkl.gz', # 数据集文件
                    nkerns=[20, 50],        # 每隐层特征图数目序列
                    batch_size=500):        # mini-batch大小（for MSGD）
    
    # 加载数据，生成训练集/验证集/测试集
    datasets = load_data(dataset)
    
    train_set_x, train_set_y = datasets[0]
    valid_set_x, valid_set_y = datasets[1]
    test_set_x,  test_set_y  = datasets[2]
	...
	# 搭建模型网络结构（包括上面的隐层sizes推导）

	# 输入
    layer0_input = x.reshape((batch_size, 1, 28, 28))

	# 第一层 - 复合
    layer0 = LeNetConvPoolLayer(
        rng,
        input=layer0_input,
        image_shape=(batch_size, 1, 28, 28),
        filter_shape=(nkerns[0], 1, 5, 5),
        poolsize=(2, 2)
    )
    
	# 第二层 - 复合
    layer1 = LeNetConvPoolLayer( ... ) 

	# 第三层 - 隐层   
    layer2_input = layer1.output.flatten(2)
    layer2 = HiddenLayer( ... )

	# 全连接输出   
    layer3 = LogisticRegression(input=layer2.output, n_in=500, n_out=10)

    # 似然损失函数
    cost = layer3.negative_log_likelihood(y)
	...
    # 参数更新机制
    updates = [
        (param_i, param_i - learning_rate * grad_i)
        for param_i, grad_i in zip(params, grads)
    ]

	# 模型训练函数体
    train_model = theano.function(
        [index],
        cost,
        updates=updates,
        givens={
            x: train_set_x[index * batch_size: (index + 1) * batch_size],
            y: train_set_y[index * batch_size: (index + 1) * batch_size]
        }
    )
    
    ########## 模型训练 ##########

	# 早停机制设置
    patience = 10000  # 迭代次数耐心上限
    patience_increase = 2  # 耐心上限拓展步长
    improvement_threshold = 0.995  # 精度明显提升判断

	# 验证周期
    validation_frequency = min(n_train_batches, patience // 2)
	...    
	# 循环
    while (epoch < n_epochs) and (not done_looping):
        epoch = epoch + 1

		# mini-batch迭代
        for minibatch_index in range(n_train_batches):
			...
			# 模型训练（损失计算+参数更新）
           	cost_ij = train_model(minibatch_index)

			# 模型验证（a batch训练完成）
            if (iter + 1) % validation_frequency == 0:

                # 计算0-1损失 - 验证误差
                validation_losses = [validate_model(i) for i in range(n_valid_batches)]
                this_validation_loss = numpy.mean(validation_losses)
				...

                # 如果取得更好模型（验证精度提升）
                if this_validation_loss < best_validation_loss:
					# 若精度提升明显，但耐心迭代次数上限达到，则提高迭代次数上限
                    if this_validation_loss < best_validation_loss * improvement_threshold:
                        patience = max(patience, iter * patience_increase)
					...

					# 进行测试（在验证精度提升时）以方便我们对比观测
                    test_losses = [
                        test_model(i)
                        for i in range(n_test_batches)
                    ]
                    test_score = numpy.mean(test_losses)
					...

			# 早停判断
            if patience <= iter:
                done_looping = True
                break
    	...
	#返回所需信息

训练及测试

这里采用MSGD（块随机梯度下降法）进行迭代寻优，下图是经过大约5万次迭代训练后得到的三种误差（训练/验证/测试）收敛曲线，可以看出其过程收敛性：

样例图片

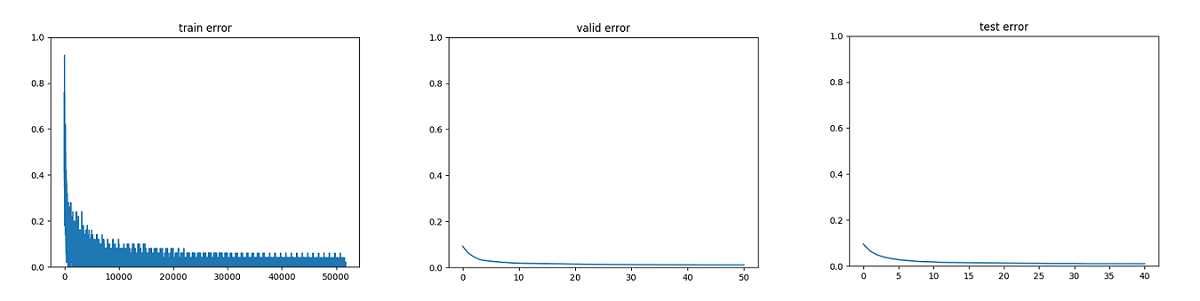
显示出一些测试样本的预测结果如下图示：

样例图片

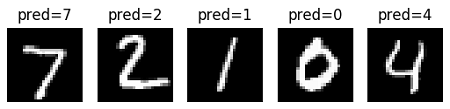
最终的运行结果打印如下:

# 最优验证误差结果
Best validation score of 1.080000 %
# 测试误差结果
Test performance 1.030000 %
# 过程时耗
The code for file Mnist_CNN.py ran for 90.23m

从这里的结果可以看出：一方面，卷积神经网络训练计算规模庞大（当前软硬件环境下耗时一个半小时）；另一方面，得到的模型精度很高（在测试集上实现了约99%的精度，这基本意味着MNIST问题得到了解决）。

总结

通过该实验，我们注意到：

  • CNN是一种优秀的机器学习模型，能够实现较困难的学习任务；
  • 以CNN为代表的“深度学习”模型的训练往往面临着巨大的计算量，为优化实现，一方面需要提升软硬件配置环境，另一方面要合理设计训练机制，包括MSGD、早停、正则化等辅助方法的合理运用；
  • 参数设置合理与否严重影响模型的训练效率和实现效果；

通过该实验，我们回顾了卷积神经网络及其所代表的深度学习概念，练习了基于python-theano计算框架下的机器学习建模方法，为进一步的学习研究积累的实践经验。

参考

下面列出相关参考：